Ementas
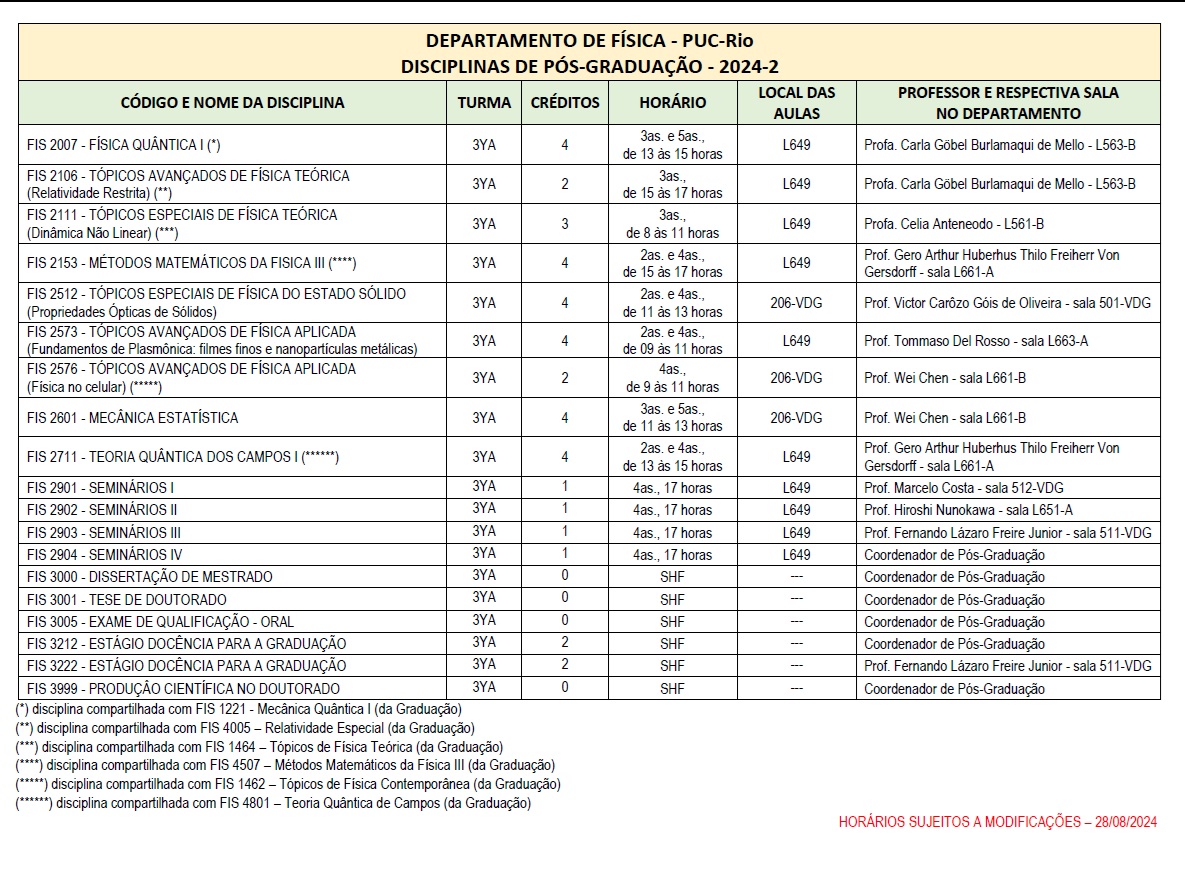
FIS 2106 – Tópicos Avançados de Física Teórica
(Relatividade Restrita)
Turma 3YA – 2 créditos – Horário: 3as., de 15 às 17 horas, sala L649
Profª. Carla Göbel
A física pré-relativística: Transformações de Galileu e Relatividade Newtoniana. As equações de Maxwell e a questão do éter. O experimento de Michelson-Morley e tentativas de explicar seu resultado nulo.
O Princípio da Relatividade. Transformações de Lorentz e consequências: relatividade da simultaneidade, dilatação temporal, contração de Lorentz. Intervalo invariante; diagrama espaço-tempo: cone de luz, causalidade. Transformação de velocidades. Transformação de frente de onda e Efeito Doppler relativístico.
O espaço-tempo quadri-dimensional: métrica de Minkowski. Quadri-vetores, Tensores, Transformações de Lorentz formais. Dinâmica da Partícula, relação massa/energia, lei de força relativística. Processos relativístivos: colisões, decaimentos.
Eletrodinâmica relativística. Conceitos do eletromagnetismo: Equações de Maxwell, potenciais escalar e vetor, invariância de Gauge. O eletromagnetismo em forma covariante: equações com fontes e sem fontes. Força de Lorentz. Invariantes eletromagnéticos.
Tensor energia-momento. Exemplos.
Bibliografia:
- Introduction to Special Relativity, Wolfgang Rindler, 2nd , Oxford University Press.
- Special Relativity and Classical Field Theory, Leonard Susskind and Art Friedman, Hachette Book Group.
- Introducing Einstein’s relativity, Ray D’Inverno, Oxford University
FIS 2111 – TÓPICOS ESPECIAIS DE FÍSICA TEÓRICA
(Dinâmica Não Linear e Caos)
Turma 3YA – 3 créditos – Horário: 3as., de 08 às 11 horas, sala L649
Profª. Celia Anteneodo
Sistemas não lineares em 1 e 2 dimensões. Análise de estabilidade linear. Bifurcações. Ciclos limite. Resolução numérica de equações diferenciais. Seção de Poincaré e mapas discretos. Mapa logístico. Expoente de Lyapunov. Rotas para o caos. Sistemas dinâmicos. Sistema de Lorenz. Espectro de Lyapunov. Aplicações a sistemas mecânicos, elétricos, biológicos, etc.
Bibliografia:
- SH Strogatz; Nonlinear dynamics and chaos.
- MW Hirsh, S Smale, RL Devaney; Differential equations, dynamical systems and an introduction to chaos.
- KT Alligood, TD Sauer, JA Yorke; Chaos: and introduction to dynamical systems.
FIS 2153 – MÉTODOS MATEMÁTICOS DA FÍSICA III
Turma 3YA – 4 créditos – Horário: 2as. e 4as., de 15 às 17 horas, sala L649
Prof. Gero Arthur Hubertus Thilo Freiherr Von Gersdorff
PRÉ-REQUISITO(S): FIS1506 (Métodos Mat. Fís. Eng. II) ou FIS4506
OBJETIVO
O curso de Métodos Matemáticos da Física III tem como objetivo aprofundar o conhecimento dos conceitos principais da matemática utilizada na física contemporânea. Os tópicos apresentados na disciplina são fundamentais na aprendizagem da teoria de campos quânticos, relatividade geral, matéria condensada, etc.
EMENTA
Método da função de Green avançada e funções especiais avançadas, Grupos e álgebras de Lie (grupos SO(n), SU(n), Sp(n) e suas álgebras, representações), Geometria diferencial (variedades, forma diferencial, geometria de Riemann, geometria conforme, teorias de calibres).
PROGRAMA
Método da função de Green em coordenadas esféricas e cilíndricas. Funções especiais (funções Gamma, Bessel, Bessel modificada, Legendre, Hermite, Hipergeométrica). Identidade de funções especiais, representações de Rodrigues e Schläfli. Definição de Grupo, conceitos básicos. Exemplos de grupos, grupos contínuos e de Lie. Grupos de Lie clássicos (SO(n), SU(n), Sp(n), O(p,q), SL(n), U(p,q), etc). Representação de grupos de Lie. Álgebra de Lie e representação. Definição de variedade, cálculo na variedade (formas, tensores). Variedade de Riemann (métrica, transporte paralelo, conexão, curvatura, vetor de Killing, spinores).
AVALIAÇÃO
Critério 3
BIBLIOGRAFIA PRINCIPAL
Mathematical Methods for Physicists, 6th edition, G.B. Arfken, H.J. weber, Elsevier Academic Press (2005).
Geometry, Topology and Physics, M. Nakahara, CRC press, 2nd edition (2003).
Mathematical Physics: A Modern Introduction to Its Foundations, Sadri Hassani, 2nd edition, Springer Nature (2013).
BIBLIOGRAFIA COMPLEMENTAR
Mathematical Physics: A Modern Introduction to its Foundations, S. Itassani, Spring, (2013).
Differential Geometry and Lie Groups for Physicists, M. Fecko, Cambridge University Press, (2006).
The Geometry of Physics, T. Frankel, Cambridge University Press, 3rd edition (2011).
Lie algebras in particle physics: from isospin to unified theories, H. Georgi, CRC press, 2nd edition (2018).
Classical groups for physicists, B. Wybourne, John Wiley and Sons Inc (1974).
FIS 2512 – TÓPICOS ESPECIAIS DE FÍSICA DO ESTADO SÓLIDO
(Proriedades Ópticas de Sólidos)
Turma 3YA – 4 créditos – Horário: 2as. e 4as., de 09 às 11 horas,
sendo 2as., na L649 e 4as., na 206 do VDG
Prof. Victor Carôzo Gois de Oliveira
Resumo:
O curso abrange os princípios fundamentais e tópicos avançados relacionados à interação da luz com materiais no estado sólido. O curso começa com uma visão geral da teoria eletromagnética da luz e sua interação com a matéria. A seguir, o curso vai explorar a relação entre estrutura eletrônica e propriedades ópticas, incluindo conceitos como éxciton, plasmons e polaritons.
O curso então avança para várias técnicas experimentais para medir propriedades ópticas de sólidos, como espectroscopia de absorção, medições de refletividade e as espectroscopias Raman e de fotoluminescência. Atenção especial é dada fenômenos de óptica não linear no final do curso.
Após a conclusão deste curso, os alunos terão adquirido uma compreensão abrangente das propriedades ópticas dos sólidos e serão capazes de aplicar esse conhecimento a uma ampla gama de pesquisas e aplicações em ciência dos materiais, física da matéria condensada e espectroscopia óptica.
Sumário:
Introdução
- Propagação clássica da luz
- Absorção interbandas
- Excitons
- Luminescência
- Confinamento quântico
- Elétrons livres
- Fônons
- Óptica não linear
Bibliografia:
- Optical Properties of Solids, Mark Fox, 2010, second edition, Oxford University Press.
- Solid State Physics, Ashcroft, N. W. and Mermin, N. D., Thomson learning.
FIS 2573 – TÓPICOS AVANÇADOS DE FÍSICA APLICADA
(Fundamentos de Plasmônica: filmes finos e nanoparticulas metálicas)
Turma 3YA – 4 créditos – Horário: 2as. e 4as., de 09 às 11 horas, sala L649
Prof. Tommaso Del Rosso
A interação entre a radiação eletromagnética e metais pode provocar sob oportunas circunstancias a excitação coletiva dos elétrons livres, suportando ondas de plasma de volume e superfície. Essas ultimas são de particular interesse devido ao atual estado da arte na fabricação de nanoestruturas e filmes finos, permitindo a excitação de plasmons de superfície seja estacionários que propagativos. Em ambos os casos, as oscilações coletivas dos elétrons permitem a concentração da radiação eletromagnética além do tradicional limite de difração, com importantes consequências em uma vasta gama de aplicações como microscopia e sensoriamento ótico de alta resolução, aprisionamento ótico, foto-catálise e nanomedicina.
O curso pretende dar uma panorâmica geral da área da plasmonica, mostrando como seja possível, a partir das equações de Maxwell, confinar a radiação eletromagnética além do limite de difração em interfaces metal-dielétricas. Serão mostrados os aspectos teóricos e as implicações tecnológicas das espectroscopias óticas amplificadas pela superfície, com ênfase na área do (bio-)sensoriamento ótico e aplicações biomédicas. Serão em fim abordadas as principais técnicas de fabricação de filmes finos, nanopartículas e nanoestruturas metálicas. São previstas demonstrações experimentais.
Parte 1 – Propriedades óticas dos metais. Feixes Óticos Gaussianos e limite de difração. Ressonância de plasmon de superfície (SPR) em interfaces metal-dielétricas. Conceito de curva de dispersão em plasmons propagativos. Guias de ondas óticas planares. Sensores SPR propagativos: aspectos físicos e químicos. Bio-sensores Plasmonicos..
Demonstrações Laboratoriais: espectroscopia SPR e fabricação de filmes finos metálicos.
Parte 2 – Técnicas de fabricação de nanopartículas e nanoestruturas metálicas com ênfase na ablação por laser pulsado. Conceito e medida da extinção ótica. Seção de choque de extinção de nanopartículas. A aproximação quase estática (AQE). Ressonância de plasmon localizada (LSPR). Além da AQE. Interação entre nanopartículas de metais nobres. Sensores Óticos LSPR: aspectos físicos e químicos. Espectroscopia Raman amplificada pela superfície (SERS). Aplicações biomédicas: terapia térmica para câncer e regeneração de tecidos.
Demonstrações Laboratoriais: síntese e caracterização ótica de nanopartículas metálicas.
Bibliografia
1) H. Raether, Surface Plasmons on Smooth and Rough Surfaces and on Gratings, Springer Tracts in Modern Physics (Springer-Verlag, 1988).
2) S.A. Maier, Plasmonics: Fundamentals and Applications, Springer US, 2007.
3) M. Quinten, Optical Properties of Nanoparticle Systems: Mie and Beyond, (Weinheim: Wiley), (2011), doi: 10.1002/9783527633135.ch2.
FIS 2576 – TÓPICOS AVANÇADOS DE FÍSICA APLICADA
(Física no Celular)
Turma 3YA – 2 créditos – Horário: 4as., de 09 às 11 horas na sala L649
Prof. Wei Chen
Nossos telefones celulares, computadores e outros dispositivos eletrônicos do dia-a-dia usam muitos princípios físicos da mecânica clássica, mecânica quântica, eletromagnetismo, e física do estado sólido. Esta aula tem como objetivo apresentar os princípios-chave por trás desses dispositivos modernos.
Espera-se que os alunos tenham cursado Estrutura da Matéria I.
Os tópicos possíveis incluem:
- Elétrons em uma rede, condutividade.
- Magnetorresistência gigante, histerese, torque de transferência de spin.
- Semicondutores, transistor de efeito de campo, células solares, LED.
- Resposta eletromagnética de sólidos, absorção óptica.
- Cristais líquidos, polímero condutivo, grafeno.
- Sensores de movimento e giroscópio.
- Relatividade especial e GPS, metamateriais e antena.
- Movimento browniano na bateria.
- Noções básicas de aprendizado de máquina.
Referências:
Solid State Physics – N. W. Ashcroft and N. D. Mermin, 1976.
Principles of Quantum Mechanics – R. Shankar, 2011.
Principles of Condensed Matter Physics – P. M. Chaikin and T. C. Lubensky, 2012.
Solid State Physics – J. R. Hook and H. E. Hall; Wiley, 1995.
Introduction to Statistical Physics – S. Salinas, 2001.
Neural Networks and Deep Learning: A Textbook – C. C. Aggarwal, 2018.
